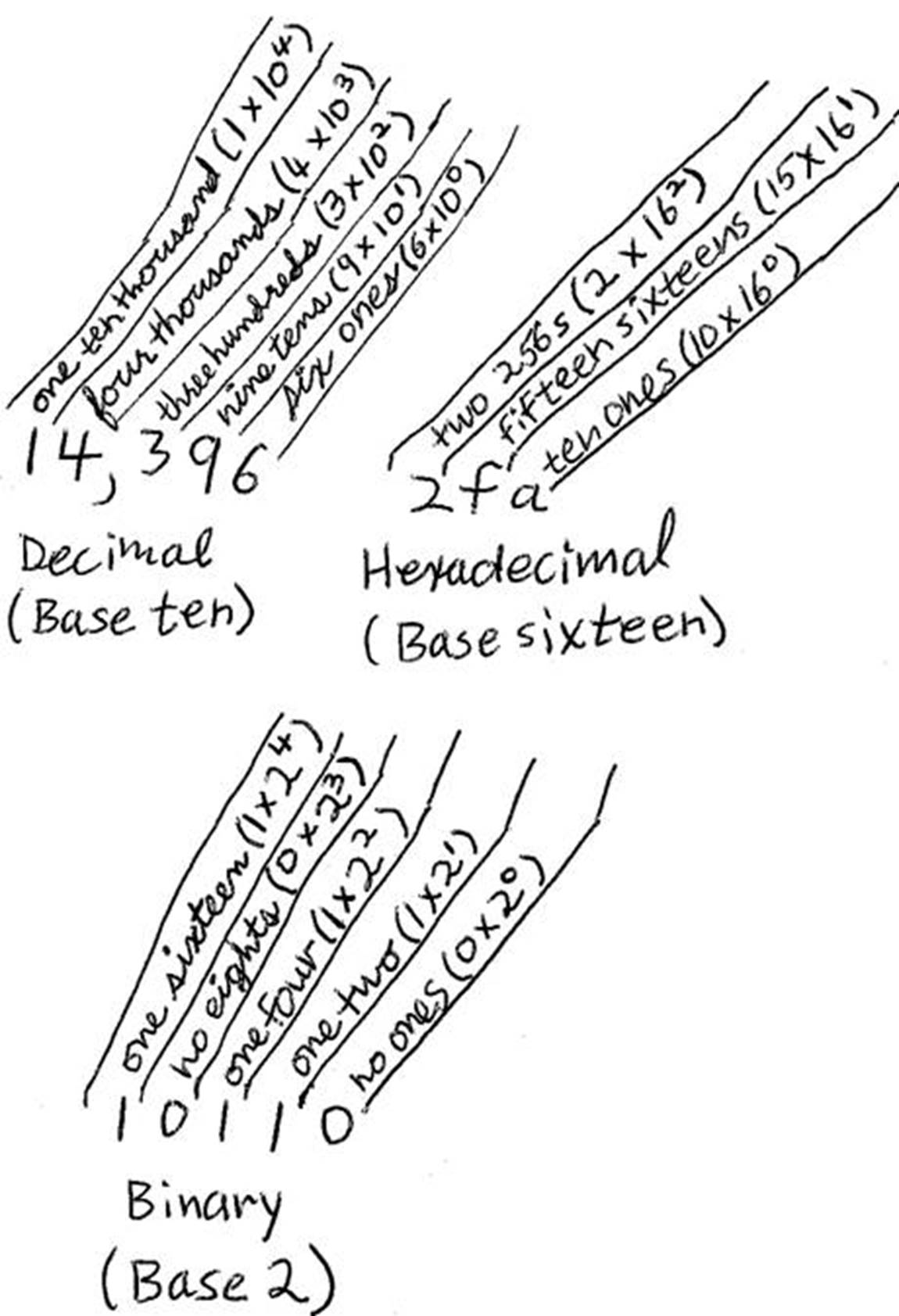
Base 10 (Decimal System),
Base 16 (Hexadecimal System), and
Base 2 (Binary System)
Let's check how numbers work
Historically there are other ways (1, 2)
Typical modern numbers follow a specific system
Consider a number like 365
3 hundreds, 6 tens, and 5 ones
This is for base 10, works for others too
Why is base 10 so widely used?
Here are formats of numbers in bases 10, 16, and 2
The ones column
Why does N0 = 1?
N3 = N*N*N
N2 = N*N
N1 = N
N0 = ???
N-1 = 1/N
N-2 = 1/(N*N)
Making it work
Divide 103 by 10
103 = 10*10*10 = 1000
103/10 = 102 = 100
102/10 = 101 = 10
101/10 = 100 = 1
100/10 = 10-1 = 1/10 = 0.1
10-1/10 = 10-2 = (1/10)/10 = 1/100 = 0.1/10 = 0.01
10-2/10 = 10-3 = (1/100)/10 = 1/1,000 = 0.01/10 = .001
Notice we now have columns for tenths, hundredths, ...
Why do we call it base 10?
There are 10 numeral symbols
1, 2, 3, 4, 5, 6, 7, 8, 9, ?
We left out 0!
What about hexadecimal numbers?
Base 16
"hex-" means 6
"decimal" means 10
So "hexadecimal" means 16
"hex" is slang for hexadecimal
"hexagecimal" is a less popular name
Making "hex" work
We need 16 numeral symbols
Here they are:
1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, ?
What is missing?
So A = ten
B = eleven
C = twelve
D = thirteen
E = fourteen
F = fifteen
Columns work the same way as base 10
Rightmost column is for 160 = 1s
Next column is for 161 = 16s
3rd column from the right is for 162=256s
4th is for 163=4098s
Could decimal points and columns to their right make sense?
Next, what about binary (base 2)?
We need 2 numeral symbols
Let us call them
0
1
Binary numbers have columns too
They work the same way
3rd from the right column
22 = 2*2 = 4s
(options: 0 or 1 4s)
4th column is for 23 = 8s
5th column is for 24 = 16s
2nd column is for 21 = 2s
Rightmost column is for 20 = 1s
The number two has
One 2 and zero 1s
So, 10
Conversion from one base to another
Let's convert 1111112 into decimal
0b111111.toString(10);
0b111111.toString();
The rightmost column contains 1 20=1
The next column contains 1 21=2
The third column contains 1 22=4
The 4th contains 1 23=8
The 5th contains 1 24=16
The leftmost contains 1 25=32
Add'em up!
1+2+4+8+16+32, or 6310
Converting base 16 to base 10
Example: convert 3b7 into decimal
0x3b7.toString(10);
0x3b7.toString();
Rightmost column contains seven 160=1s
Next column contains b (that is, eleven) 161=16s
Left column contains 3 162=256s
Add'em up!
7*1+11*16+3*256=951
So 3b716 = 95110
Going the other way: base 10 to base 16
Example: 100 (one hundred)
(100).toString(16);
What is it in hex?
How many 161 = 16s go into 100?
If over 15 of them, start with 162 = 256s
6 of them do: 16*6 is 96, remainder 4
96 is accounted for
4 is unaccounted for
Let's account for it
How many 160 = 1s go into 4?
4 of them do
Is the answer ...
6416 or 4616?
Check: 6*16+4*1=100
Another example: 256 into hex
Another example: 273 into hex
Converting base 10 into binary
Process is analogous
Example: 10010 to binary
(100).toString(2);
Start with the highest (left) column
27=128 which does not fit into 100
So there is no 8th digit
If one is needed, pad with 0
In decimal, 042 and 42 are the same number
128s column is blank (or 0)
26=64 fits into 100 once
Lucky! If it was 2 or more, we made a mistake
Put a 1 in the 64s column
Removing 1*64=64 from further consideration
Remainder is 100-64=36
25=32 fits into 36 once
Put 1 in the 32s column
Remove 1*32 from the 36, leaving 4
24=16 does not fit into the remaining 4
Put 0 in the 16s column
Likewise for the 23=8s column
22=4 does fit into 4
Put 1 in the 4s column
Remove 1*4 from the remaining 4
This leaves 0 left to account for
21=2 does not fit in 0
So 21 column gets 0
20=1 does not fit in 0
So 20 column gets 0
Thus, 10010 is 11001002
Another example: 3
Another example: 2
Another example: 7