Safe and Effective Computer Arithmetic

By Daniel Berleant, Dept. of Electrical and Computer Engineering, Iowa State University

A review of Scientific Computing, Validated Numerics, Interval Methods (Joint Proceedings of SCAN 2000 and Interval 2000), ed. by W. Krämer and J. von Gudenberg, Kluwer Academic/Plenum, 2001.

Computers were invented to do tedious arithmetic calculations dependably, yet several decades later this goal has still not been reached. The world of arithmetic on computers is a world of approximations, where even simple numbers like 1/3 are usually represented inaccurately, and where the risk of inaccuracies building up over the course of a computation means that the goal of dependability continues to be a fruitful and worthy area of study. Fortunately significant progress continues to occur, as shown by this rich and diverse snapshot of the state of the art.

The transition from binary coded decimal to floating point hardware early in computing history was performance driven. Still today, speed trumps numerical accuracy in hardware comparisons, though Lorenz’ renowned weather model (1963) signaled the birth of chaos theory and a new understanding of the potentially dramatic implications of even tiny numerical inaccuracies. Hence Walster’s description (p. 6) of “Moore’s fear” – Murphy’s law run rampant in “mission critical applications.” We refer of course to Ramon (Ray) Moore, the grandfather of the interval computing community, a community heavily committed to improving dependability of computations by representing values safely with lower and upper bounds.

This volume contains numerous chapters that attest to both the vigor and the maturity of validated numerical computing. Many chapters deepen understanding of such traditional topics as linear algebra, global optimization, control, and differential equations. Other chapters attest to the dynamism and practical relevance of the field by addressing diverse other topics as well. Here are a few examples.

Hyvönen examines several candidate notations for intervals for use in commercial products, each with its own advantages and disadvantages. The one best meeting requirements of user friendliness and informativeness for printed intervals in computer output might be termed delta-tilde notation. Here, a key parameter is delta, the maximum precision level relevant to the application, expressed as a negative whole power of 10. If the need to format either interval bound in limited space requires rounding it so much that the proportion of rounding error exceeds delta, then that bound is displayed with a tilde immediately following. Hence [1.2443, 1.2574], formatted to fit in a small space, could print as [1.2~,1.3~]. This conclusion is implemented in a commercially available interval extension to the Excel spreadsheet software.

Kulpa takes a quite different approach to interval display by investigating graphical rather than character-based displays. In particular, he investigates display of an interval as a point in a 2-D coordinate space, where the horizontal axis expresses the midpoint of the interval and the vertical axis expresses its width (more specifically its half-width, or radius). The paper notes that these midpoint-radius (MR) diagrams can be used to expose interesting characteristics of intervals and operations on them, contradicting the dominant Hilbert-style view that diagrammatic methods lack the formalizability needed to be of significant mathematical interest.

Three chapters address control. Although the control field is relatively mature and sophisticated, validated methods have interesting contributions to make. In so doing, the control field contributes as well, by providing a rich collection of examples upon which to (1) demonstrate validated methods, (2) exercise their capabilities, and (3) motivate further advances in validated methods whose need the examples highlight. Heeks, Hofer, Tibken, Lunde, and Thorwart address the important problem of uncertainty in sensor output, showing that interval-based global optimization can guarantee acceptable performance of a fly-by-wire aircraft elevator model. Krastanov and Dimitrova address a methane-producing bioreactor system. Given several system parameters of uncertain value, they model the uncertainties with interval bounds, then deduce a quadrilateral in the space of concentrations of substrate and biomass within which optimality cannot be ruled out. They then derive a feedback control procedure to keep the system operating in that region and successfully test it via numerical simulation.

Another example of the variety and vigor of work on validated computing is the growing body of results relating to probability. Alt and Markov describe advances in stochastic arithmetic. Vamos, Suciu, Vereecken, Nitzsche, and Hardelauf explain how they achieved a speedup of three orders of magnitude in simulating an important class of diffusion problems. Ferson, Ginzburg, Kreinovich, and Schulte establish an interesting result about uncertainty classes, which are sets of probability distribution functions. They view an interval as representing the set of all probability distributions whose samples are guaranteed to fall within the interval, and observe that p-bounds – envelopes bounding a space within which distributions are permitted to travel (see Figure 1) – are only one variety of uncertainty class. They proceed to prove that any uncertainty class can be described arbitrarily closely by the distribution of some random variable, an interval expressing the range of another, independent random variable, and a function that takes as arguments samples of these two random variables.

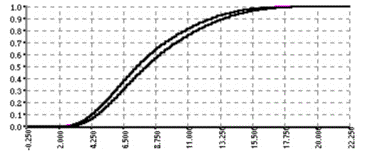
Figure 1: P-bounds. These consist of a pair of probability distributions enclosing a space defining the set of all probability distributions whose curves do not leave that space.

Oddly, the results of Michelucci on reliable determination of strange attractors are categorized under the heading of stochastics and probability, although it is precisely the determinism of nonlinear, chaotic systems that challenges our understanding. Such systems, though deterministic, can be so sensitive to perturbations that the numerical inaccuracies typical of computer arithmetic lead to results that diverge rapidly from what they would be if no inaccuracy was present. Michelucci describes how interval methods can produce validated conclusions about strange attractors, and shows that the classical method of determining them can lead to conclusions that are significantly, even dramatically, incorrect. And now we can come full circle. Early in this review a simple non-linear weather model was noted, described by Lorenz who conjectured it to be a chaotic system with a strange attractor (nonperiodic but with repeating characteristics). Using interval arithmetic for validated computations, Tucker (2002) has recently proved that this system does indeed possess a strange attractor, a proof listed as the fourteenth of Smale’s (1998) mathematical challenges for the 21^st century.

References

Lorenz, E. N., Deterministic nonperiodic flow , Journal of the Atmospheric Sciences 20 (1963), 130-141.

Smale, S., Mathematical problems for the next century, Mathematical Intelligencer 20, no. 2 (1998), 7-15.

Tucker, W., A rigorous ODE solver and Smale’s 14^th problem, Foundations of Computational Mathematics 2:1 (2002), 53-117.